오늘 리뷰할 논문은 GAN으로 더 잘 알려진, 적대적 인공신경망을 처음으로 제안한 논문이다.
뭐 이미 말할 필요도 없이 유명하기도 하고, 수많은 variation이 나오기도 했다.
논문의 제 1저자인 이안 굿펠로우는 GAN의 generator를 지폐위조범으로, discriminator를
경찰로 묘사했다. 지폐위조범은 위조 지폐를 더욱 더 진짜 같이 위조하고, 경찰은 그걸 구분하려고
경쟁하는 과정에서 상호발전이 일어난다는 것이다. 사실 우리의 목표는 경찰보다는
지폐위조범의 생성능력을 상승시키는 것에 있다. 결국 학습의 끝에서는 경찰이
어느 것이 위조 지폐인지 진짜 지폐인지 알아볼 수 없도록 말이다.
이렇듯 기본적인 아이디어는 굉장히 직관적이지만, 이론적 배경은 꽤나 탄탄하다.
이제 차근차근 하나씩 알아보겠다.
GAN을 알아보기 전, VAE에 대해서 먼저 잠깐 짚고 넘어가자.
VAE의 가장 큰 문제점은 blurry한 이미지가 생성된다는 것이다.
여러가지 설명이 있을 수 있겠지만, 필자가 생각하기로는 VAE의 loss function에서
기인한다고 생각한다.
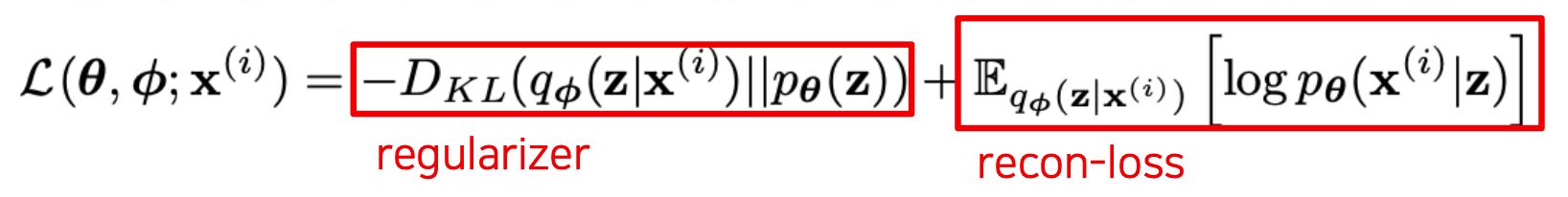
첫 번째 term은 $q_{\phi}(z|x)$가 prior $p_{\theta}(z)$와 너무 달라지지 않게
조절하는 regularization term이고 두 번째 term은 latent factor $z$로 부터 원래의 데이터
$x$를 복원하는데서 생기는 loss에 해당한다. 사실 두 번째 term은 회귀분석의 식과
정확히 일치한다.
$y = X\beta + \epsilon$라는 가정에서 출발한다. 이때 입실론은 평균이 0, 표준편차가 $\sigma$인
정규분포를 따른다. 우리는 $x_{i}^{T}\beta$와 $y_{i}$의 오차를 줄여주고 싶기 때문에
최적화된 파라미터는 다음 수식을 만족한다.
$\hat{\beta} = argmin_{\beta} {||y-X\beta||^{2}}$
$\epsilon$이 정규분포를 따르기 때문에 $y$도 정규분포를 따르게 된다.
즉, $N[X\beta, \sigma^{2}]$를 따른다. 이때 Maximum Likelihood 방식으로 $\beta$를
구하게 되면 다음과 같다.

결국 LSE로 구한 방법과 MLE로 구한 방법이 같아지고, 이는 앞에서 본 VAE의 손실 함수에서
두 번째 term에 해당한다. L2 loss를 줄이기 위해서 linear regression은 target의
평균으로 예측하는 경향이 있기 때문에 VAE로 생성된 함수는 흐려지는 것이다.
그에 비해 GAN으로 생성하는 이미지는 굉장히 sharp하다. 그럼 이제 수식을 하나하나
알아보도록 하겠다.
0. Objective Function

GAN을 학습하는 과정은 결국 이 minimax 문제를 푸는 것이라 할 수 있다.
D 입장에서는 진짜 데이터일때(첫 번째 term) 진짜라고 예측할 확률을 극대화(1)하고,
G가 생성한 가짜 데이터일때(두 번째 term) 진짜라고 예측할 확률을 극소화(0)하여
objective function 값이 커져야 한다.
G 입장에서는 D가 생성한 데이터를 진짜로 판별할 확률 $D(G(z))$을 극대화하여
$log(1-D(G(z)))$를 극소화해야하기 때문에 objective function 값이 작아져야 한다.

하지만 이렇게 gradient descent/ascent 방법을 적용하면 문제가 있다.

위의 그래프를 보면, G가 제대로 못하는 상황에서 gradient가 작고 잘하는 상황에서
gradient가 크기 때문에 학습이 원활히 이루어지지 않음을 알 수 있다.
따라서 실제로 학습을 할 때는

이런 식으로 바꾼 다음 gradient를 적용한다고 한다.
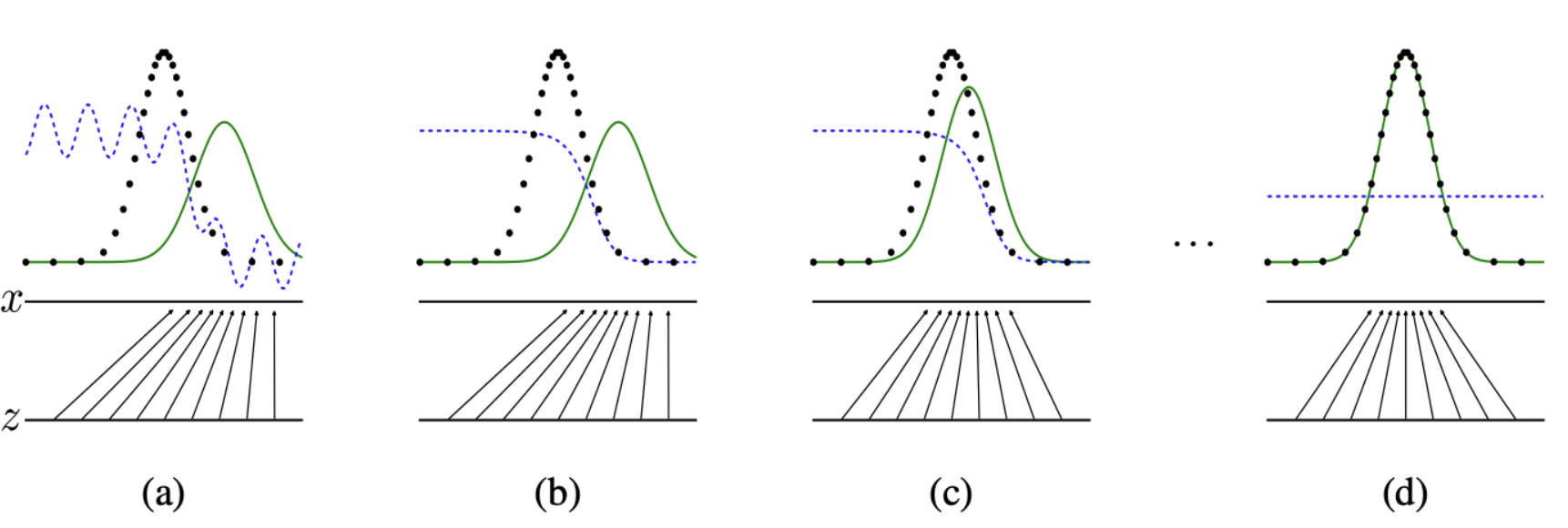
(a)에서는 generator가 제대로 mapping을 못하고 있고, D도 given G에 대해서 optimal하지 않다.
(b) D goes to optimum for given G
(c) G converges to data distribution
(d) global optimum에 도달. G는 데이터의 분포를 완벽히 학습했고 D는 그냥 찍기가
되어버렸다.
그렇다면 실제로 이렇게 학습이 되는지 수식적으로 살펴보도록 하겠다.
1. Global Optimality

먼저, G가 주어졌을 때 D의 optimum은 (2)와 같다는 주장이다. LaTex로 옮기기
귀찮아서.. 내가 쓴 풀이과정은 아래와 같다.

사실 인테그랄을 빼고 뭐 합치고 이런 과정에서 뇌피셜이 꽤나 들어가서.. 정확한 풀이인지는
모르겠지만 대략 위처럼 구할 수 있다.
그러면 이제 optimal D에 도달했다고 하고 G에 대해서 최적화를 해보자.
위의 식을 $C(G)$로 바꾸고, $C(G)$를 minimize하는 G가 존재하는지,
그렇다면 그 G는 어떤 G인지 알아보자.

위의 식을 하나하나 풀면 아래와 같다. 사실은 그냥 $log(4)$를 더하고 뺀 트릭일 뿐...
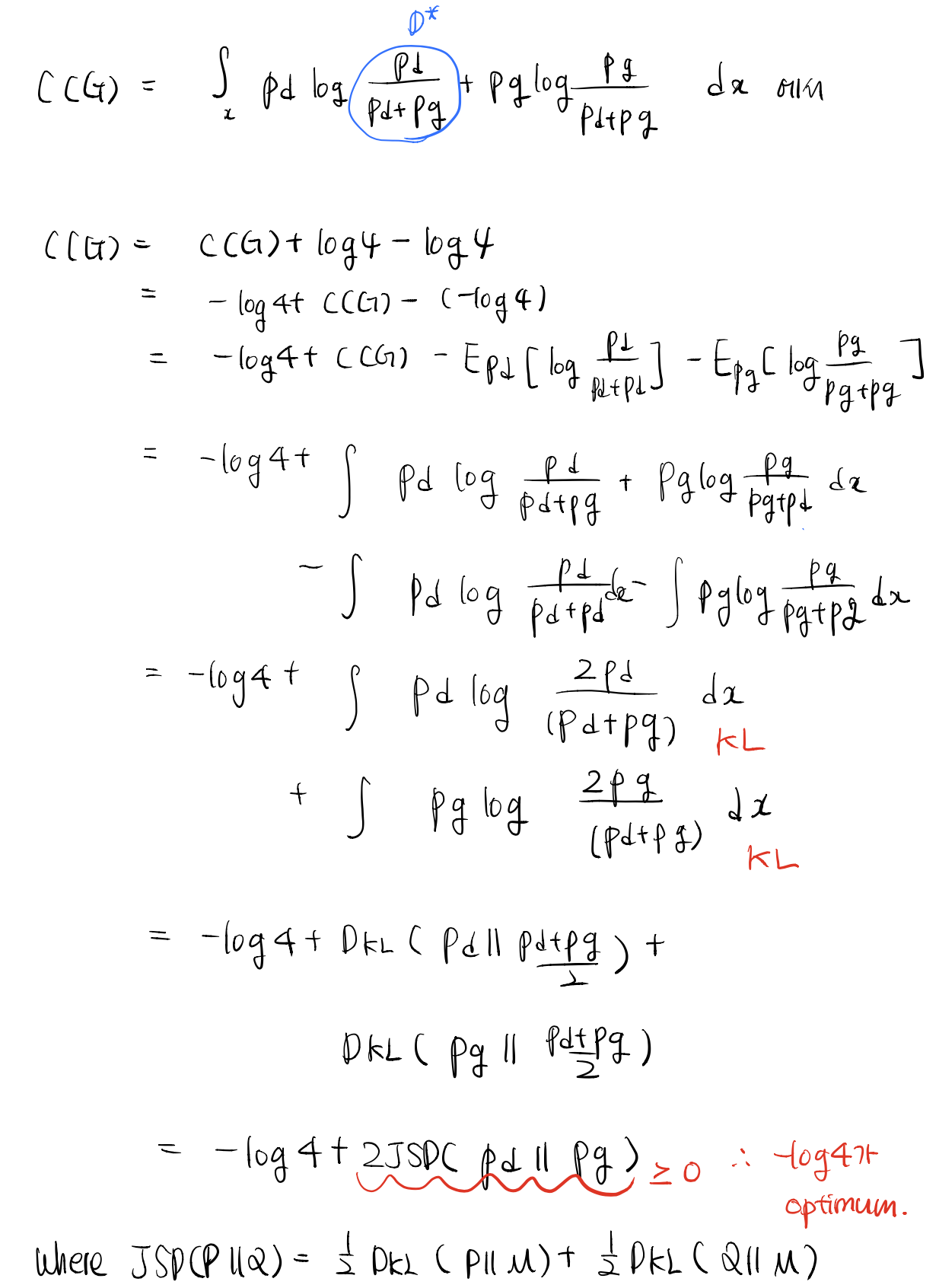
결국, $p_{g} = p_{d}$를 만족하는 G가 optimal G가 되고 이때 optimum value는
$-log(4)$에 해당한다.
최적의 값이 존재한다는 것과 알고리즘으로 값을 찾을 수 있다는 다른 문제기 때문에,
이제 algorithm에 대한 convergence를 증명해야 한다. 이 문제는 매우 간단하게 증명된다.
2. Convergence of Algorithm

위의 식을 $p_{g}$에 대해서 미분하면 $log(1-D_{G}^{*}(x))$만 남기 때문에 $p_{g}$에 대해서
convex하고, gradient descent에 의해 $p_{g}$는 $p_{data}$로 수렴한다.
지금까지 GAN의 이론적 근거에 대해서 알아보았다.
요약하자면
-
1) given G에 대해서 D의 optimum D* 존재, D가 수렴(1차 미분으로 풀 수 있음)
-
2) D*에 대해서 G가 수렴: $p_{g}$가 $p_{d}$를 만족할 때 까지..
-
3) repeat 1), 2) until converged
다음은 GAN으로 생성된 이미지들이다.

중간중간 부자연스러운 것들도 보이지만, 대체로 학습이 잘되었다.
그렇다면 GAN은 항상 완벽한 generation을 할 수 있을까? 그건 아니다.
대표적으로 다음과 같은 문제들이 존재한다.
-
minimax 학습으로 인한 학습의 불안정성, mode collapsing
-
함수 공간을 neural network로 정의하면 함수 공간이 아닌 parameter space가 되기 때문에 가정이 깨짐
첫 번째에 대해서 알아보자면, neural network 입장에서는 이게 minimax인지 maxmini인지
알 길이 없다. 따라서 D가 최적화되지 않은 상태에서 G를 최적화하게 되면
G는 D가 제일 헷갈리는 샘플만 내놓으면 된다. 또한 data distribution이 여러 개의
mode가 있을 때(예를 들어, MNIST에서는 숫자 1-10이 이에 해당한다)
G 입장에서는 1만 완벽하게 생성해도 D가 헷갈리기 때문에 학습이 완료된다.
(물론 이때 D는 다른 숫자들에 대해서 판별능력이 구리다)
사실 GAN의 불안정한 학습을 해결하기 위해 여러 방법들이 고안되었고,
지금도 이에 대해서 활발히 연구가 진행되고 있다고 한다.
given G에 대해서 D를 optimize하는 것이 만만치 않기 때문에 그렇다.
두 번째는 보다 일반적인 얘기이다. 위의 모든 증명들은 함수 공간에서 성립하는
증명인데, 사실 우리는 FC layer, Convolution layer 등 네트워크를 설계하고
parameter를 최적화한다. 물론 인공신경망이 universal function approximator라는 것은
잘 알려져 있지만, 우리가 설계한 네트워크가 $f$에 맞을지는 모르는 일..
reference: GAN paper, jaejunyoo.blogspot.com/2019/05/part-i.html
'ML, DL > 논문 리뷰' 카테고리의 다른 글
| DeepFM: A Factorization-Machine based Neural Network for CTR Prediction 리뷰 (0) | 2022.03.06 |
|---|---|
| Auto-Encoding Variational Bayes 리뷰 (0) | 2020.11.09 |
| GPT-1 리뷰: Improving Language Understanding by Generative Pre-training (0) | 2020.09.30 |
| Why Should I Trust You? 리뷰 (0) | 2020.09.22 |
| Empricial Evaluation of Gated Recurrent Neural Networks On Sequence Modeling 리뷰 (0) | 2020.09.17 |