VAE로 잘 알려진 Auto-Encoding Variational Bayes를 리뷰해보려고 한다. 이 논문은
Auto-Encoder를 보다 probabilistic한 관점으로 접근한 논문으로,
black box 모델이라고 생각되어지는 neural network를 확률적인 시각으로
볼 수 있다는 아이디어를 제시했으므로 통계학과인 나에게는 더 특별하게(?) 다가왔다.
논문 초록에 의하면, 이 논문은 intractable한 posterior를 가지는 경우에
variational lower bound를 reparameterization하여 그것을 바로 optimize함으로써
stochastic gradient방법으로 해결할 수 있다고 한다. 또한, approximate posterior
inference를 적합함으로써 posterior inference를 할 수 있다고 제시하고 있다.
1. Introduction
우리가 가지고 있는 데이터의 변수들이 continuous latent factor($z$)를 가지고 있다고 가정하자.
$p(z|x)$, 즉 posterior 분포는 거의 대부분 경우에서 intractable하다. 왜냐하면
marginal 분포를 계산하는 과정에서 적분이 생기고, 모든 latent factor에 대해서
이 적분을 실행하는 것은 무리기 때문이다.
이 논문에서는 i.i.d dataset(independently and identitically distributed) 데이터와
continuous latent variable을 가정하고 이 가정에 대해 Auto-Encoding VB 알고리즘을
제시한다. 이에 대해서는 뒤에서 살펴볼 예정이다. 이 알고리즘은 SGVB estimator를
사용해서 단순한 샘플링 하나만으로 model parameter를 효과적으로 학습할 수
있고 이 방법은 MCMC와 다르게 매우 time effective하다.
2. Method
여기서의 핵심은 a lower bound estimator를 derive하는 것이다.
일단 우리 모델이 다음과 같다고 가정한다.
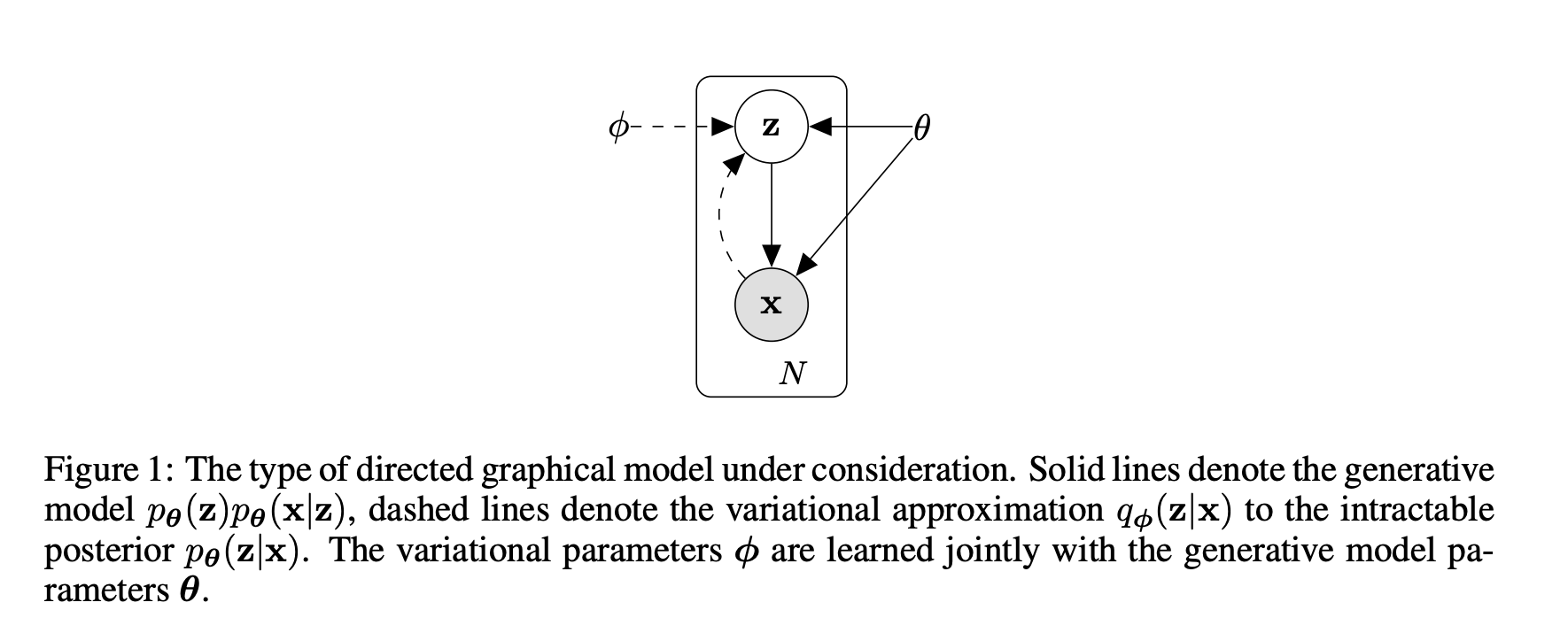
2.1 Problem Scenario
데이터 생성과정은 다음과 같다.
$p_{\theta^{*}}(z)$에서 $z$ 생성 => $p_{\theta^{*}}(z|z)$에서 $x$ 생성
그러나 이 경우 우리는 $\theta^{*}$를 모르고, $z^{i}$도 실제로는 모른다. 따라서
이 논문에서는 이러한 약점을 극복하기 위해 marginal, posterior을 모른다고 가정하고
보다 일반적인 경우에서 작동할 수 있는 알고리즘을 설계했다.
목표는 다음과 같다.
1) ML/MAP estimation for the general parameters $\theta$
2) $p(z|x)$ inference
3) $p(x)$ inference
일단, posterior를 구할 수 없기 때문에 $q_{\phi}(z|x)$를 posterior의 approximation으로
둔다. 다시 말해 이 확률분포는 encoder, $p(x|z)$는 decoder가 된다.
2.2 The Variational Bound
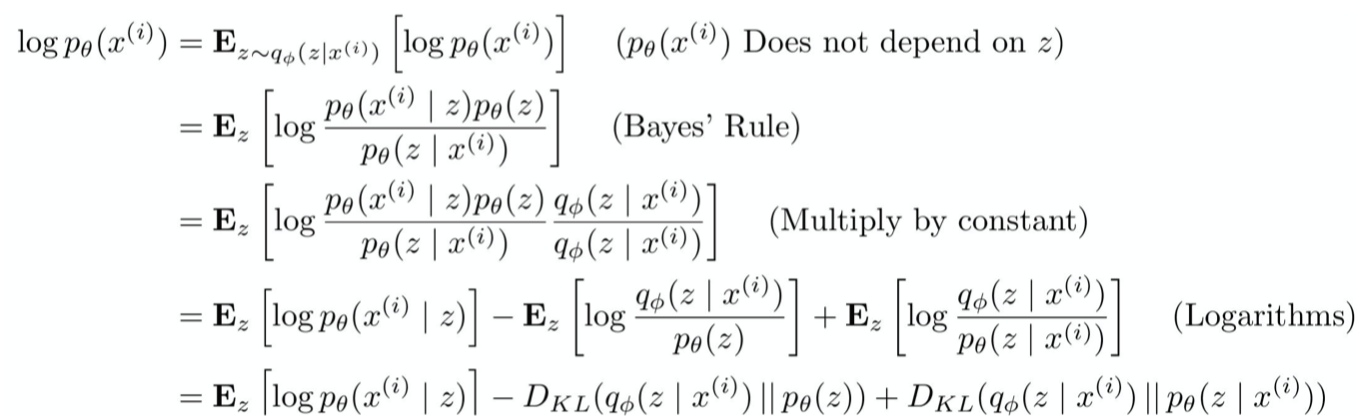
해당 그림은 cs231n 슬라이드에서 가져온 것으로, 하나하나 잘 풀어져있어서 그대로 넣었다.
맨끝 KL term은 intractable posterior의 식을 알아야 하므로 생략하는데,
중요한 것은 항상 0이상이 된다는 것이다. 따라서 lower bound는 다음과 같다.
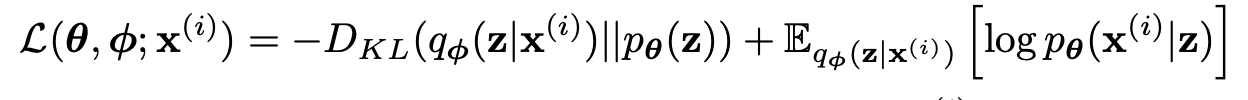
앞부분은 prior과 approximate posterior와의 KL term이고, 뒷부분은 decoder probability에
해당한다.
decoder에 대해서는 reparameterization 부분에서 다시 설명하겠다.
2.3 The SGVB estimator and AEVB algorithm
$q_{\phi}(z|x) \rightarrow \tilde{z} = g_{\phi}(\epsilon, x)$
위에 나온 식이 바로 reparameterization의 핵심 트릭이다. 여기서 $\epsilon$은 랜덤
노이즈에 해당한다. 위의 식에서 바로 Monte Carlo estimate를 구할 수 있다.
이 알고리즘은 크게 두 갈래로 나뉘는데,
1) $x, z$의 joint probability에서 sampling
2) $p(x|z)$, conditional probability에서 sampling
직관적으로도 후자가 더 효율적&직관적이므로, 실제로는 두번째 방법을 썼다고 한다.
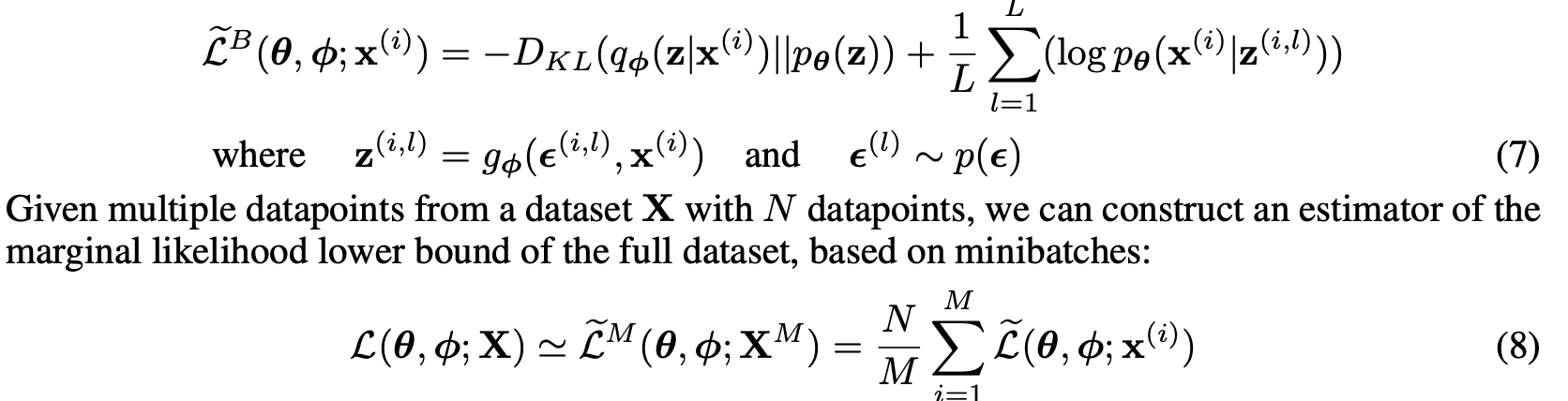
논문에 따르면 (7)의 식에서 첫번째 term은 approximate prior에 대한 regularizer, 뒤의 term은
expected negative reconstruction error에 해당한다.
일단 여기까지 읽으면 $g_\phi$는 어떻게 구하지?라는 의문점이 드는데, 그에 대한 해답은
다음 섹션에 나와있다.
2.4 The Reparameterization Trick ~ 3.Example: Variational Auto-Encoder
수식이 많이 나와 혼란스럽지만 하나하나 따라가다보면 어려운 내용은 아니다.
1) $p_{\theta}(z)$가 다변랑 표준 정규분포(모평균은 0벡터, 모분산은 1벡터를)따른다고 가정하자.
물론 모델에 따라서 바이노미알 분포가 될 수도 있고, 지수 분포가 될 수도 있다.
2) $p_{\theta}(x|z)$는 다변량 정규분포로 가정한다.
3) posterior는 approxiate normal을 따른다고 가정한다.
그렇다면 $q_{\theta}(z|x)$는 다음과 같이 모델링 할 수 있다.
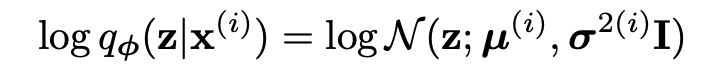
이때, $\mu^{i}, \sigma^{2(i)}$는 MLP layer를 통해 나온 output이기 때문에,
우리는 여기서 $exp(\epsilon)$만 $\sigma^{2(i)}$에 곱해주면 된다. 이때, $\epsilon$은
다변량 표준 정규분포를 따른다. 이렇게 나온 결과값 $z$를 decoder에 넣어준다.
이게 바로 reprameterization의 끝이다! 생각보다 간단하고, 구현된 코드를 보면 이게 전부이다.
(다만 논문에서와 다르게 구현된 코드는 대부분 $\epsilon$을 한 번만 샘플링한다는거..
논문에서는 $L$번 샘플링한다고 나와있다.)
또한 회귀분석에 대해 공부해본 적이 있는 사람이라면 매우 직관적이다.
여튼 이러한 방법으로 end-to-end가 backpropagation이 가능하게 된다.
(원래 $q(z|x)$에서 샘플링을 하게 되면 미분가능한 연산이 아니게 된다.)
간단하게 언급하자면, $y$변수(타겟변수)가 $x$변수(feature)와 linear한 관계에 있다고
가정하고 $y = ax+b+\epsilon$식에서 $a, b$를 푸는 것인데
결국 이는 $p(y|x)$를 구하는 태스크가되고 $x$는 given, $a, b$는 constant라고
가정하기 때문에 random factor은 $\epsilon$ ~ $N(0, 1)$에서만 생긴다.
즉, $p(y|x)$는 $ax+b$를 평균으로하고 1을 분산으로 하는 정규분포가 된다.
따라서 $a, b$는 MLE 방법으로 closed-form solution이 나오게 된다.
지금까지 설명한 VAE와 개념적으로 상당히 비슷함을 알 수 있다.
논문에서는 $g$가 되기 위한 세 가지 좋은 조건(tractable inverse CDF,
location-scale family, composition)도 언급하는데 이는 생략하겠다.
4, 5번 섹션에서는 그냥 다른 latent factor modeling 알고리즘보다 더
잘나왔다고 하는 그래프가 거의 전부라서.. 이것도 생략..
+) VAE의 단점인 blurry generation을 짚고 넘어가려고한다.
approximate posterior가 regularizer 역할을 하고, reconstruction loss가 실제
cost에 해당한다고 볼 수 있기 때문에 $logp(x|z)$를 높이는 방향으로 학습이 된다.
이는 일종의 Linear Regression(MLE)으로 볼 수 있고, 결국 $x$의 평균과
가까워지게 된다. 따라서 VAE로 생성된 이미지는 보다 흐리다.
+) 기존의 AE와 다른점은 posterior가 $p(x)$를 그대로 외워버리지않게
posterior, prior의 KL term을 추가한 것(regularization)
지적, 질문 모두 환영합니다! :)
이 글에서 쓰인 모든 이미지는 원본 논문에서 캡처한 것이며, 원본 논문의 링크는 우측에 있습니다. [링크]
'ML, DL > 논문 리뷰' 카테고리의 다른 글
| DeepFM: A Factorization-Machine based Neural Network for CTR Prediction 리뷰 (0) | 2022.03.06 |
|---|---|
| Generative Adversarial Nets 리뷰 (0) | 2020.11.20 |
| GPT-1 리뷰: Improving Language Understanding by Generative Pre-training (0) | 2020.09.30 |
| Why Should I Trust You? 리뷰 (0) | 2020.09.22 |
| Empricial Evaluation of Gated Recurrent Neural Networks On Sequence Modeling 리뷰 (0) | 2020.09.17 |