1. Introduction
Language Modeling은 NLP에서 항상 중요한 태스크로 자리잡아왔다.
Word2Vec, RNNLM 부터 ELMO, BERT까지 Language Modeling에 해당하는 모델들로,
단어에 대한 good representation을 찾고자 했다.
다만, long-term dependency를 포착하는 것이 중요하나 쉽지 않았다.
Vanilla RNN에서는 gradient vanishing/explosion 문제가 있었고,
이를 해결하기 위해 LSTM, gradient clipping technique 등이 등장했지만 insufficient 했다고 한다.
따라서 어텐션만 사용하는 트랜스포머만 사용하여 LM을 훈련시키고자 하는 시도가 있었고
대체로 LSTM 계열의 모델보다 잘 작동했지만 긴 sequence에 대해서 fixed-length를 가진 부분들(segments)로 나누어서
모델이 훈련되었다. 즉, predefined context length를 넘는 longer-term dependency는 잡을 수 없었다.
또한, fixed length를 가진 segment는 문장/의미 기준으로 나누어지지 않았기 때문에 문맥적인 정보가 부족했다.
이를 context fragmentation problem이라고 해당 논문에서는 칭하고 있다.
위에서 언급한 문제들에 대한 해결책으로 저자들은 크게 두 가지 방안을 제시하고 있다.
첫 번째는 recurrence mechanism이다. 즉, 전 segment에서 얻어진 hidden state를 현재 segment의 memory를 사용함으로써 segmentsr간에 recurrence connection을 구축하는 것이다.
두 번째는 relative positional encoding으로 기존 트랜스포머 모델에서 사용한 positional encoding(sinusoid formulation)이
토큰의 절대적인 위치를 인코딩했다면 해당 논문에서는 토큰의 상대적인 위치를 인코딩하고 있다.
이 두 가지에 대해서 천천히 알아보도록 하자!
3. Model
기본적으로 LM은 $P(x) = \prod{P(x_{t}|x_{<t})}$이라는 조건부 확률을 구하는 것이다. 다시 말해 어떤 시퀀스가 주어졌을 때
다음에 올 단어/토큰을 예측하는 모델이라고 할 수 있다. 전통적인 방법은 $t$시점까지의 context를 고정된 길이의 벡터로 인코딩한 후, word embedding과 곱해 logit을 구하는 것이다.
3.1 Vanilla Transformer Language Models

위의 그림은 vanilla transformer lm으로 max seq length가 4라고 가정하고 학습/평가 과정을 도식화하여 보여준 것이다.
학습시 max sequence length 단위로 segment를 잘라서 학습하고
평가시에는 $x_{t}$를 예측할 때 $x_{t-4}$부터 $x_{t-1}$를 사용하게 된다.
이 경우, 크게 3가지의 문제가 생기게 된다.
1. 정보가 흐르지 않는다.(forward, backward 모두 마찬가지)
2. 가장 긴 dependency length가 segment length로 제한된다.
3. context fragmentation
3.2 Segment-Level Recurrence with State Reuse
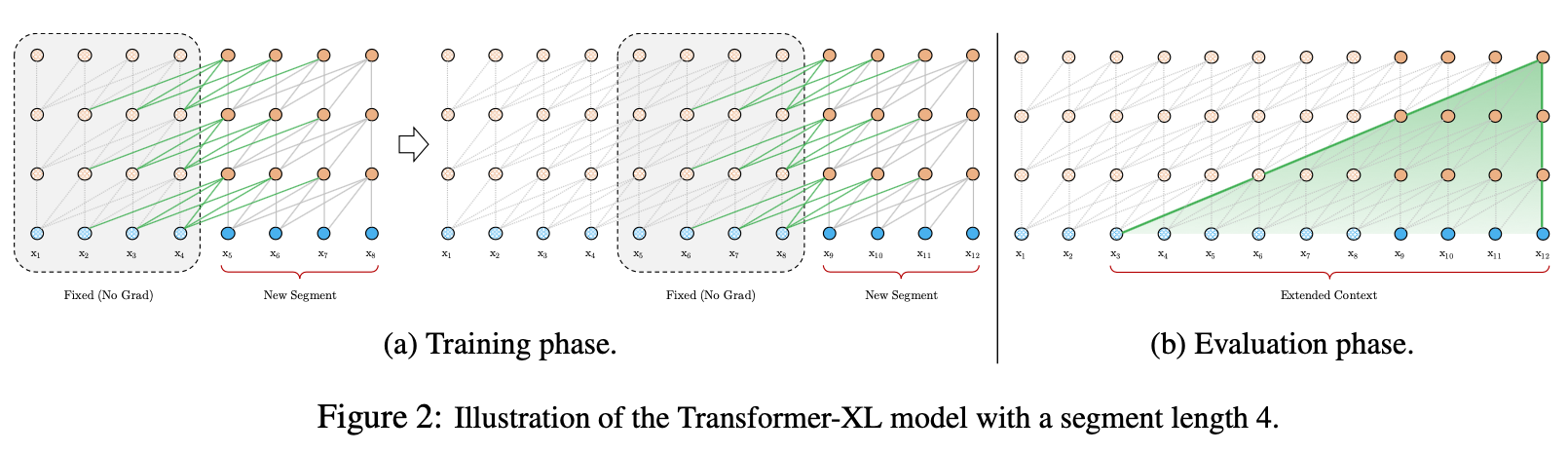
앞서 말한 3가지의 문제점을 해결하기 위해 해당 논문의 저자들은 전 segment에서 계산된 hidden state를 caching하여 새로운 segment를 훈련시킬 때 사용했다고 말한다. 이 때 전 segment의 hidden state는 gradient를 freeze시키기 때문에
학습의 대상이 되지 않는다. 찬찬히 수식을 살펴보도록 하겠다.
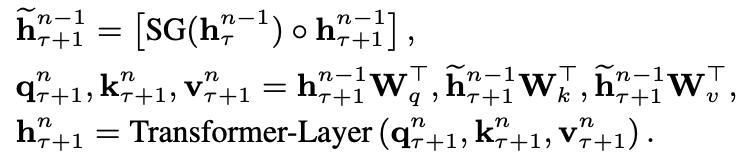
$\tau+1$번째 segment의 $n$th layer hidden state는 위와 같이 구해진다.
$\tilde{h_{\tau+1}^{n-1}} = \text{extended context}$라고 논문 저자들은 명명하고 있고
$SG$는 stop-gradient의 약자로 그라디언트를 흘려보내지 않는다는 뜻이다.
여기서 주목해야 할 점은 key, value 부분으로 query와 다르게 key, value가 전 segment의 $n-1$번째
layer의 hidden state를 가지고 있다는 것이다.
또한 기존의 RNN 계열 LM은 recurrence가 같은 순서의 레이어안에서 진행된 것에 비해 해당 모델은
one-layer downwards recurrence를 가진다.
이 모델의 장점은 다음과 같다.
1. 이론상 가장 긴 dependency length $O(L \times N)$을 가진다. 여기서 L은 segment length, N은 layer의 개수이다.
2. faster evaluation
3. GPU가 허락하는 한 최대한 많은 previous segments를 cache할 수 있고,
실제로 평가시에는 학습시에 사용한 cache의 배수만큼 사용했다고 한다.
3.3 Relative Positional Encodings

기존의 트랜스포머는 인풋 임베딩과 sinusoid formulation을 이용한 positional encoding의 element-wise sum으로
이루어졌으나 이를 그대로 사용하면 segment 정보에 상관없이 $j$번째 토큰의 positional encoding이 항상
같아진다는 문제점이 생긴다.
사실 positional encoding은 단어가 어떻게 모여서 문맥을 형성하는지에 대한 bias를 나타낸다.
cf) inductive bias
이 bias를 어텐션 스코어에 포함시키면 어떨까? 라는 생각에서 착안하여 relative positional encoding을 개발하였다고 한다.
쿼리와 키의 절대적인 위치정보($i, j$)가 아니라 상대적인 위치정보 - 즉, 거리($i-j$)만 포함하기 때문에
relative라는 단어가 붙었다.
이를 나타내는 행렬 $R$을 만들고, $i$번째 행은 두 위치간 relative distance를 나타낸다고 한다. 이 행렬을
만들때는 sinusoid formulation을 사용하였다.


1. (b)=>(d): $U_{j} \rightarrow R_{i-j}$, relative distance만이 어떤 곳에 attend할 지 중요하다는 가정을 반영한다.
2. (c)=>(d): $u, v \in \mathbf{R^{d}}$가 학습되는 파라미터로 추가되었고, query의 절대적인 위치 정보는
어떤 곳에 attend할 지 중요하지 않다는 가정을 반영한다.
3. $W_{k}$가 $W_{k, E}$와 $W_{k, R}$로 분리: content-based key vector & location-based key vector
요약하자면 다음과 같다.
(a): content-based addressing
(b): content-dependent positional bias
(c): global content bias
(d): global positional bias

그 다음부터는 기존 트랜스포머랑 다를 것 없다.
4. Experiments
4.2 Main Results

4.2 Ablation Study

Attn Len이 길어짐에 따라 longer dependency modeling이 가능해졌다.
recurrence mechanism, relative positional encoding 모두 중요함을 볼 수 있다.

longer dependency가 없는 코퍼스에 대해서도 좋은 성능을 보였고 이는 recurrence mechansim이
context fragmentation 문제를 해결한다고 해석할 수 있다. 그리고 relative positional encoding이 짧은 시퀀스에 대해서도
더 좋은 성능을 보였다고 한다.
4.3 Relative Effective Context Length
ECL(Effective Context Length): context span을 늘렸을 때 threshold 이상의 gain을 얻을 수 있는 가장 긴
length
하지만 ECL은 shorter context를 이용한 모델의 perplexity가 작다는 점을 고려하지 않아 공정한 비교가 가능하지 않다.
이에 논문의 저자들은 RECL(Relative Effective Context Length)라는 새로운 지표를 제시한다.
이는 한 모델 그룹 안에서 정의된 기준으로, 긴 context length의 이점은 best short context model(baseline model)의
상대적인 성능 향상으로 측정된다. 그리고 이 지표는 $r$이라는 파라미터를 가지는데
이는 비교를 top-r hard examples로 한정한다.

이건 학회에서 논문 발제를 맡으면서 만들었던 ppt의 일부인데, 원본 논문의 식을 그대로 참조했다.
3번에서 잘못말한게, $l_{i}(c', t))$를 빼먹었다...ㅠ $c'$는 $c+\Delta$로 더 긴 context length를 말한다.
모델 그룹안에서 가장 성능이 뛰어난 모델과 비교했을 때의 결과이므로, 3번 수식의 결과에 $l_{i}(c', t))$이 많으면
긴 context length의 정보가 잘 담긴다는 뜻이다.

RECL을 구하는 실제 알고리즘인데 감소율을 사용하고 있는 이유는 직관적으로 알 수 있고, $exp$를 사용한 이유는
아마 $l_{i}(c', t))$가 negative log likelihood기 때문에 $exp$을 취해야 실제 확률값이 나오고
소프트맥스에서 $exp$를 사용하기 때문이 아닐까..?라고 생각하고 있다.
지적, 질문 모두 환영합니다! :)
이 글에서 쓰인 모든 이미지는 원본 논문에서 캡처한 것이며, 원본 논문의 링크는 우측에 있습니다. [링크]
'ML, DL > 논문 리뷰' 카테고리의 다른 글
| Generative Adversarial Nets 리뷰 (0) | 2020.11.20 |
|---|---|
| Auto-Encoding Variational Bayes 리뷰 (0) | 2020.11.09 |
| GPT-1 리뷰: Improving Language Understanding by Generative Pre-training (0) | 2020.09.30 |
| Why Should I Trust You? 리뷰 (0) | 2020.09.22 |
| Empricial Evaluation of Gated Recurrent Neural Networks On Sequence Modeling 리뷰 (0) | 2020.09.17 |